Chapitre 3 exercice 47
Page 1 sur 1
 Chapitre 3 exercice 47
Chapitre 3 exercice 47
Bonjour! Est-ce que quelqu'un pourrait m'expliquer comment faire le numéro 3E47, car je ne sais pas comment déterminer si le tuyau est ouvert ou fermé en (a) et je n'ai pas encore essayer le (b) car j'aimerais d'abord comprendre le (a)...J'ai utilisé les 2 fourmules pour tuyau ouvert et fermé mais je ne sais pas comment exploiter les résultats que j'obtiens. J'ai trouver la vitesse avec les 2 fréquences v=f * longueur d'onde(j'ai pris 0.45 m), mais ensuite je ne suis pas sûre. Merci de me répondre! 
Invité- Invité
 Piste Chap 3 numéro 47
Piste Chap 3 numéro 47
Bonsoir Sarah
Comment peut-on savoir si le tuyau est ouvert ou fermé ? Il faut d'abord se rappeler la principale différence entre un tuyau ouvert et un tuyau fermé au niveau des POSSIBILITÉS d'harmoniques. Dans un des deux, toutes les harmoniques sont possibles et dans l'autre seuls les harmoniques impairs sont possibles. D'après toi, lequel est lequel ?
Il faut faire attention au mot mode, car ça peut porter à confusion. Dans un tuyau OUVERT, étant donné que toutes les harmoniques sont possibles (oups j'ai donné la réponse), le mode correspond à l'harmonique. Par exemple, le premier mode est la fondamentale, le deuxième mode constitue le 2e harmonique, le troisième mode est le 3e harmonique, etc. Par contre dans un tuyau FERMÉ, le mode correspond-t-il au "numéro" d'harmonique ? Je te conseille de revoir la page 70 du Benson si cette notion t'a échappé !
Troisièmement, si l'on fait le rapport (le quotient) des fréquences de modes consécutifs avec la formule f=nv/2L ou f=nv/4L (ça ressemble drôlement au problème),
on devrait toujours arriver à une harmonique de valeur entière (pas un nombre à virgule).
Je vais commencer une solution et si tu as compris, tu pourras la continuer:
Tuyau Ouvert
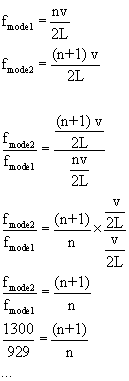
Si ça ne fonctionne pas avec le tuyau ouvert, essaie avec le tuyau fermé. Attention, l'harmonique du mode consécutif dans le cas d'un tuyau fermé vaut-il (n+1) ?
Vincent
Comment peut-on savoir si le tuyau est ouvert ou fermé ? Il faut d'abord se rappeler la principale différence entre un tuyau ouvert et un tuyau fermé au niveau des POSSIBILITÉS d'harmoniques. Dans un des deux, toutes les harmoniques sont possibles et dans l'autre seuls les harmoniques impairs sont possibles. D'après toi, lequel est lequel ?
Il faut faire attention au mot mode, car ça peut porter à confusion. Dans un tuyau OUVERT, étant donné que toutes les harmoniques sont possibles (oups j'ai donné la réponse), le mode correspond à l'harmonique. Par exemple, le premier mode est la fondamentale, le deuxième mode constitue le 2e harmonique, le troisième mode est le 3e harmonique, etc. Par contre dans un tuyau FERMÉ, le mode correspond-t-il au "numéro" d'harmonique ? Je te conseille de revoir la page 70 du Benson si cette notion t'a échappé !
Troisièmement, si l'on fait le rapport (le quotient) des fréquences de modes consécutifs avec la formule f=nv/2L ou f=nv/4L (ça ressemble drôlement au problème),
on devrait toujours arriver à une harmonique de valeur entière (pas un nombre à virgule).
Je vais commencer une solution et si tu as compris, tu pourras la continuer:
Tuyau Ouvert
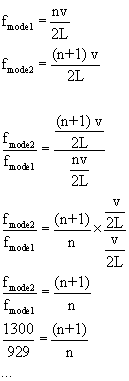
Si ça ne fonctionne pas avec le tuyau ouvert, essaie avec le tuyau fermé. Attention, l'harmonique du mode consécutif dans le cas d'un tuyau fermé vaut-il (n+1) ?
Vincent
Invité- Invité
Page 1 sur 1
Permission de ce forum:
Vous ne pouvez pas répondre aux sujets dans ce forum